目次 / Contents
1. はじめに
最尤推定法はデータから母集団のパラメータを推定する強力な手法です。
例えばコインを投げて表が出る確率を推定したいとします。
10回投げて7回表が出たとしたら、表が出る確率は7/10=0.7だと推測するでしょう。
これが最尤推定の基本的な考え方です。
しかし現実の問題はもっと複雑です。
多くのパラメータを同時に推定する必要があったり、データの分布が複雑だったりします。
そんな時に威力を発揮するのが以下の概念です。
2. 主要な概念の整理
2.1 尤度関数と最尤推定量
まず尤度関数(Likelihood function)について説明します。
尤度関数 $L(\boldsymbol{\theta})$ は、パラメータ $\boldsymbol{\theta}$ が与えられたときに観測されたデータが得られる確率(密度)を表します。
最尤推定法は、この尤度関数を最大にするパラメータ $\boldsymbol{\theta}$ を見つける方法です。
数学的には、最尤推定量 $\widehat{\boldsymbol{\theta}}$ は以下のように定義されます。
$$ L(\widehat{\boldsymbol{\theta}}) \geq L(\boldsymbol{\theta}), \quad \boldsymbol{\theta} \in \Omega $$
ここで、$\Omega$ はパラメータ空間(パラメータ $\boldsymbol{\theta}$ がとり得る全ての値の集合)を表します。
2.2 スコア関数
スコア関数(Score function)は、対数尤度関数の偏微分として定義されます。
$$ \boldsymbol{U}(\boldsymbol{\theta})=\frac{\partial l(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} $$
ここで、$l(\boldsymbol{\theta}) = \log[L(\boldsymbol{\theta})]$ は対数尤度関数です。
スコア関数は、パラメータの推定値がどの程度良いのかを示す指標として解釈できます。
スコア関数がゼロに近いほど、そのパラメータ値は尤度を最大化する値に近いと考えられます。
2.3 フィッシャー情報行列
フィッシャー情報行列(Fisher information matrix)は、スコア関数の分散共分散行列として定義されます。
$$ \boldsymbol{I}(\boldsymbol{\theta})=\mathrm{E}\left[\boldsymbol{U}(\boldsymbol{\theta}) \boldsymbol{U}^T(\boldsymbol{\theta})\right] $$
フィッシャー情報行列は、パラメータの推定精度に関する情報を表します。
直観的にはフィッシャー情報行列の値が大きいほど、そのパラメータの推定精度が高いと解釈できます。
スコア関数は確率変数ですが, Fisher 情報量はパラメータが決まれば定数になります.
3. 理論
3.1 最尤推定量の漸近正規性
最尤推定量の重要な性質の一つに漸近正規性があります。
これは、サンプルサイズが大きくなるにつれ最尤推定量の分布が正規分布に近づく性質です。
| サンプルサイズ $N$ が十分に大きいとき、最尤推定量 $\widehat{\boldsymbol{\theta}}$ は以下の分布に収束します: $$ \widehat{\boldsymbol{\theta}} \xrightarrow{d} N\left(\boldsymbol{\theta}, \boldsymbol{I}^{-1}\right) $$ ここで、$\xrightarrow{d}$ は分布収束を表し、$\boldsymbol{I}$ はフィッシャー情報行列です。 【証明】 確率変数$Y_i$ は独立な確率分布(同一でなくてもよい)に従うとします ($i=1, \ldots, N$)。 パラメータ $\boldsymbol{\theta}$ を適当な推定方程式$\begin{aligned}\sum_{i=1}^N M\left(y_i ; \boldsymbol{\theta}\right)=\mathbf{0}\end{aligned}$の解 $\widehat{\boldsymbol{\theta}}$ として求めることを考えます。 $\begin{gathered} \boldsymbol{A}=\mathrm{E}\left[-\left.\frac{\partial M\left(Y_i ; \boldsymbol{\theta}\right)}{\partial \boldsymbol{\theta}}\right|_{\boldsymbol{\theta}_0}\right] , \boldsymbol{B}=\mathrm{E}\left[M\left(Y_i ; \boldsymbol{\theta}_0\right) M\left(Y_i ; \boldsymbol{\theta}_0\right)^T\right] \end{gathered}$とします。 パラメータの値 $\theta_0$ を$\mathrm{E}\left[M\left(Y_i ; \boldsymbol{\theta}_0\right)\right]=\mathbf{0}$を満たす値として定義し、$\begin{aligned}\bar{M}(\boldsymbol{\theta})=\frac{1}{N} \sum_{i=1}^N M\left(y_i ; \boldsymbol{\theta}\right)\end{aligned}$とします。 テイラー展開により、$\bar{M}(\widehat{\boldsymbol{\theta}})$ を $\boldsymbol{\theta}_0$ の周りで展開すると、 $$\bar{M}(\widehat{\boldsymbol{\theta}}) = \bar{M}(\boldsymbol{\theta}_0) + \bar{M}'(\boldsymbol{\theta}_0)(\widehat{\boldsymbol{\theta}} – \boldsymbol{\theta}_0) + \text{remainder}$$ ここで、$\bar{M}(\widehat{\boldsymbol{\theta}}) = 0$ (推定方程式の定義より)なので、 $0 = \bar{M}(\boldsymbol{\theta}_0) + \bar{M}'(\boldsymbol{\theta}_0)(\widehat{\boldsymbol{\theta}} – \boldsymbol{\theta}_0) + \text{remainder}$ $\bar{M}^{\prime}(\boldsymbol{\theta})$ が逆行列 $\bar{M}^{\prime-1}(\boldsymbol{\theta})$ を持つと仮定すると、$\sqrt{N}\left(\widehat{\boldsymbol{\theta}}-\boldsymbol{\theta}_0\right)=-\bar{M}^{\prime-1}\left(\boldsymbol{\theta}_0\right) \sqrt{N} \bar{M}\left(\boldsymbol{\theta}_0\right)+\text { remainder }$が得られます。 $\begin{aligned}\bar{M}'(\boldsymbol{\theta}_0) = \frac{1}{N}\sum_{i=1}^N [-\frac{\partial}{\partial \boldsymbol{\theta}}M(y_i; \boldsymbol{\theta})|_{\boldsymbol{\theta}0}]\end{aligned}$ は各項の平均です。 大数の法則により、サンプルサイズ $N$ が大きくなるにつれて、この平均は期待値 $\begin{gathered} \boldsymbol{A}=\mathrm{E}\left[-\left.\frac{\partial M\left(Y_i ; \boldsymbol{\theta}\right)}{\partial \boldsymbol{\theta}}\right|_{\boldsymbol{\theta}_0}\right] \end{gathered} $に確率収束します。 $\begin{aligned}\bar{M}(\boldsymbol{\theta}_0) = \frac{1}{N}\sum_{i=1}^N M(y_i; \boldsymbol{\theta}_0)\end{aligned}$ も各項の平均です。 中心極限定理により、$\sqrt{N}\bar{M}(\boldsymbol{\theta}_0)$ は正規分布に収束します。 その平均は $\mathbf{0}$ ($\mathrm{E}[M(Y_i; \boldsymbol{\theta}_0)] = \mathbf{0}$ より)、分散共分散行列は $\boldsymbol{B} = \mathrm{E}[M(Y_i; \boldsymbol{\theta}_0)M(Y_i; \boldsymbol{\theta}_0)^T]$ となります。 ゆえに$\sqrt{N}\left(\widehat{\boldsymbol{\theta}}-\boldsymbol{\theta}_0\right)$ は確率収束する統計量と正規分布に収束する統計量の線型結合となります。 このような確率変数は, Slutskyの定理によって正規分布に分布収束します。 適当な正則条件の下で剰余項は $\mathbf{0}$ に収束します。 これらの結果を合わせることで、$\widehat{\boldsymbol{\theta}} \xrightarrow{d} N\left[\boldsymbol{\theta}_0, N^{-1} \boldsymbol{A}^{-1} \boldsymbol{B}\left(\boldsymbol{A}^{-1}\right)^T\right]$という漸近正規性が成り立ちます。 もし $\theta_0$ がパラメータの真値であるとき、 $M\left(y_i ; \boldsymbol{\theta}\right)$ を不偏な推定関数(unbiased estimating equation)といいます。 最尤推定量はスコア方程式$\begin{aligned}\frac{1}{N} \sum_{i=1}^N \boldsymbol{U}\left(y_i ; \widehat{\boldsymbol{\theta}}\right)=\mathbf{0}\end{aligned}$の解です。 スコア関数は不偏な推定関数ですので、上記の議論から$\widehat{\boldsymbol{\theta}} \xrightarrow{d} N\left[\boldsymbol{\theta}, \boldsymbol{A}^{-1} \boldsymbol{B}\left(\boldsymbol{A}^{-1}\right)^T\right]$ となります。 最尤推定量の場合は特殊なケースで, 定義からB は Fisher 情報行列$\boldsymbol{I}$そのものです。 また, $\boldsymbol{A}$ は対象 i のスコア $\boldsymbol{U}\left(y_i ; \boldsymbol{\theta}\right)$ を微分してマイナスをとったものですから, 対象1つあたりの Fisher 情報行列 $N^{-1} \boldsymbol{I}$ に一致します。 つまり $N \boldsymbol{A}=\boldsymbol{B}=\boldsymbol{I}$ が成り立つので、 最尤推定量の漸近正規性$\widehat{\boldsymbol{\theta}} \xrightarrow{d} N\left(\boldsymbol{\theta}, \boldsymbol{I}^{-1}\right)$が示されます。 |
| Slutskyの定理 サンプルサイズ $N$ のデータから計算された統計量 $L_N$ と $M_N$ があったとします。 $L_N$ は $N$ が無限大のとき $\lambda$ に確率収束するとします。 また, $M_N$ は$\sqrt{N}\left(M_N-\mu\right) \xrightarrow{d} N\left(0, \sigma^2\right)$という分布収束を满たすとします。 このとき, $L_N$ と $M_N$ の和と積は以下のように収束します. $$ \begin{gathered} \sqrt{N}\left(L_N+M_N-\lambda-\mu\right) \xrightarrow{d} N\left(0, \sigma^2\right) \\ \sqrt{N}\left(L_N M_N-\lambda \mu\right) \xrightarrow{d} N\left(0, \lambda^2 \sigma^2\right) \end{gathered} $$ |
この定理は、最尤推定量が一致性(真の値に収束する性質)と漸近有効性(サンプルサイズが大きい時、漸近的に最小分散にむかう性質)を持つことを示しています。
3.2 スコア関数、フィッシャー情報行列、観測情報行列の関係
漸近正規性という便利な性質のおかげで、われわれは 正規分布を使って $\widehat{\boldsymbol{\theta}}$ の信頼区間やp値を計算することができます。
しかし実際にはFisher 情報行列を求めなければなりません。
Fisher 情報行列の推定においてよく用いられるのは観測情報行列(observed information matrix)で代替する方法です.
観測情報行列 $\boldsymbol{i}(\theta)$ は\begin{aligned}\boldsymbol{i}(\boldsymbol{\theta})=-\frac{\partial^2 l(\boldsymbol{\theta})}{\partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T}\end{aligned}と定義されます.
| 対数尤度関数について, 微分と積分が交換可能と仮定します。 このとき, スコア関数 $\boldsymbol{U}(\boldsymbol{\theta})$ の期待値はゼロ、つまり$\mathrm{E}[U(\boldsymbol{\theta})]=\mathbf{0}$です。 また, スコア関数, Fisher 情報行列$\boldsymbol{I}(\boldsymbol{\theta})=\mathrm{E}\left[U(\boldsymbol{\theta}) U(\boldsymbol{\theta})^T\right],$観測情報行列$\begin{aligned}\boldsymbol{i}(\boldsymbol{\theta})=-\frac{\partial^2 l(\boldsymbol{\theta})}{\partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^T}\end{aligned}$には, 以下の関係が成り立ちます。 $$ \mathrm{E}\left[-\frac{\partial \boldsymbol{U}(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right]=\boldsymbol{I}(\boldsymbol{\theta})=\mathrm{E}[\boldsymbol{i}(\boldsymbol{\theta})] $$ 【証明】 簡単のため, パラメータが 1 個でデータが連続分布のときについてのみ考えます。 確率密度関数の性質から$\begin{aligned}\int p(y ; \theta) \mathrm{dy}=1\end{aligned}$です。 これを両辺について $\theta$ で微分します. $$ \frac{d}{d \theta} \int p(y ; \theta) d y=\frac{d(1)}{d \theta}=0 $$ ここで左辺は, 微分と積分が交換可能のとき$\begin{aligned}\frac{d}{d \theta} \int p(y ; \theta) d y=\int \frac{d p(y ; \theta)}{d \theta} d y\end{aligned}$となり, これはスコア関数の期待値なので$\mathrm{E}[U(\theta)]=0 $です。 次に, 上の式の左辺を微分すると, 微分と積分が交換可能であれば$\begin{aligned} \frac{d \mathrm{E}[U(\theta)]}{d \theta} & =\int\left[\frac{d}{d \theta} \frac{d l(\theta)}{d \theta} p(y ; \theta)\right] d y \\ & =\int\left[\frac{d l(\theta)}{d \theta} \frac{d p(y ; \theta)}{d \theta}+\frac{d^2 l(\theta)}{d \theta^2} p(y ; \theta)\right] d y \\ & =\mathrm{E}\left[\left(\frac{d l(\theta)}{d \theta}\right)^2\right]+\mathrm{E}\left[\frac{d^2 l(\theta)}{d \theta^2}\right] \\ & =I(\theta)+\mathrm{E}\left[\frac{d U(\theta)}{d \theta}\right] \end{aligned}$ これはゼロなので、$\begin{aligned}I(\theta)=\mathrm{E}\left[-\frac{d U(\theta)}{d \theta}\right] \end{aligned}$となります。 |
4. 具体例:二項分布
二項分布を例に、これらの概念を具体的に見てみます。
二項分布の尤度関数は
$$ L(\pi) = \binom{N}{y} \pi^y (1-\pi)^{N-y} $$となります。
ここで、$N$ は試行回数、$y$ は成功回数、$\pi$ は成功確率、$\binom{n}{k}$は二項係数です。
パラメータが 1 個のとき、最尤推定量の漸近正規性から$\begin{aligned}\operatorname{Var}(\widehat{\theta}) \approx \frac{1}{I(\theta)}\end{aligned}$ですから、標準誤差は$\begin{aligned}\mathrm{SE}(\widehat{\theta})=\left[-\left.\frac{d^2 l(\theta)}{d \theta^2}\right|_{\widehat{\theta}}\right]^{-1 / 2}\end{aligned}$となります。
これを 2 項尤度$l(\pi)=Y \log (\pi)+(N-y) \log (1-\pi)$に適用します。
$l(\pi)$ を微分すると, 1 次の導関数は以下のようになります。
$$ \frac{d l(\pi)}{d \pi}=\frac{y}{\pi}-\frac{N-y}{1-\pi} $$
フィッシャー情報行列を求めるために2 次の導関数のマイナスをとると、$\begin{aligned}-\frac{d^2 l(\pi)}{d \pi^2}=\frac{y}{\pi^2}+\frac{N-y}{(1-\pi)^2}\end{aligned}$が得られます。
これは $\pi$ が含まれているので実際に計算できません。
最尤推定量で$\pi$を置き換えると$\begin{aligned}\frac{y}{\widehat{\pi}^2}+\frac{N-y}{(1-\widehat{\pi})^2}=\frac{N}{\widehat{\pi}(1-\widehat{\pi})}\end{aligned}$となります。
この逆数の平方根をとれば$\begin{aligned}\mathrm{SE}=\sqrt{\frac{\widehat{\pi}(1-\widehat{\pi})}{N}}\end{aligned}$が導かれます。
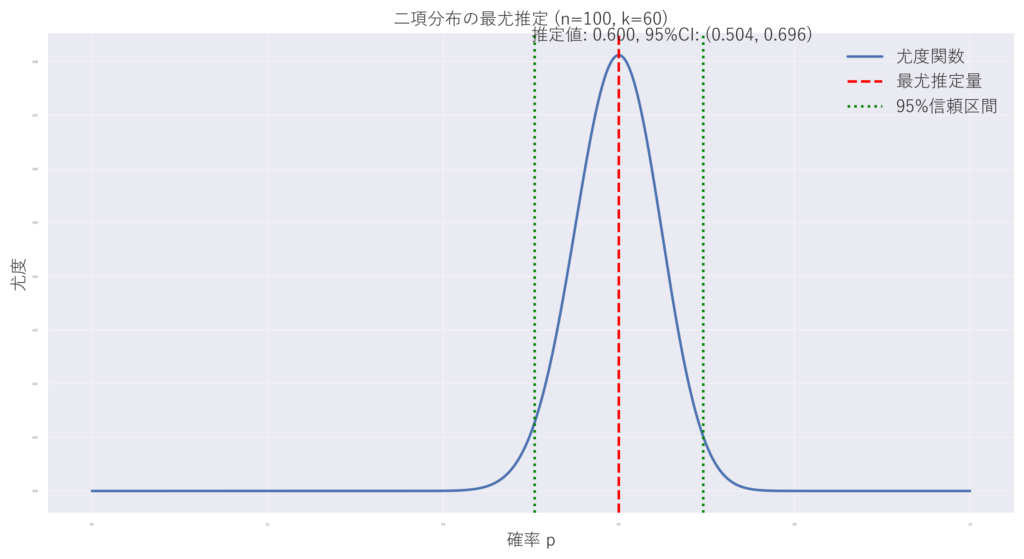
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
import matplotlib as mpl
# 日本語フォントの設定
plt.rcParams['font.family'] = 'Yu Gothic'
def plot_binomial_estimation(n, k):
p_hat = k / n
se = np.sqrt(p_hat * (1 - p_hat) / n)
ci_lower = max(0, p_hat - 1.96 * se)
ci_upper = min(1, p_hat + 1.96 * se)
p_range = np.linspace(0, 1, 1000)
likelihood = binom.pmf(k, n, p_range)
plt.figure(figsize=(12, 6))
plt.plot(p_range, likelihood, label='尤度関数')
plt.axvline(p_hat, color='r', linestyle='--', label='最尤推定量')
plt.axvline(ci_lower, color='g', linestyle=':', label='95%信頼区間')
plt.axvline(ci_upper, color='g', linestyle=':')
plt.xlabel('確率 p', fontsize=4)
plt.ylabel('尤度', fontsize=4)
plt.title(f'二項分布の最尤推定 (n={n}, k={k})', fontsize=4)
plt.legend(fontsize=4)
plt.grid(True, alpha=0.3)
plt.text(0.5, plt.ylim()[1], f'推定値: {p_hat:.3f}, 95%CI: ({ci_lower:.3f}, {ci_upper:.3f})',
horizontalalignment='center', verticalalignment='bottom', fontsize=4)
plt.show()
# 例:100回中60回表が出た場合
plot_binomial_estimation(100, 60)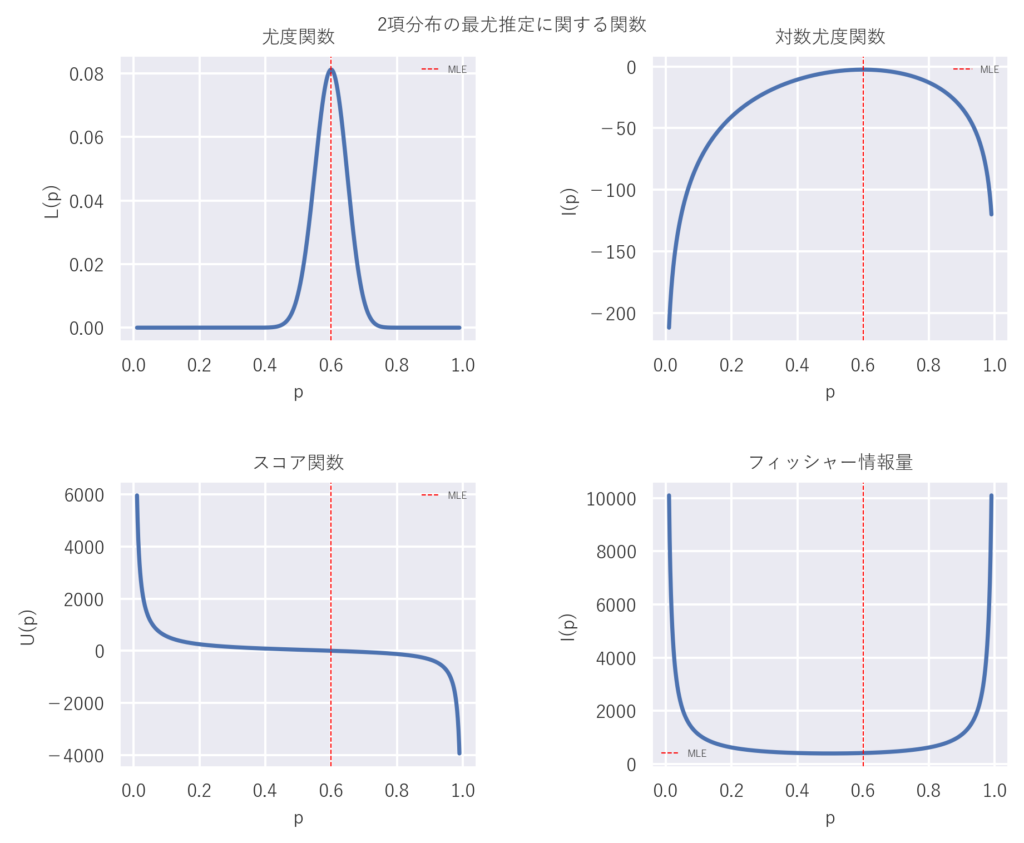
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
import matplotlib as mpl
# 日本語フォントの設定
plt.rcParams['font.family'] = 'Yu Gothic'
def plot_binomial_estimation(n, k,fontsize):
p_hat = k / n
se = np.sqrt(p_hat * (1 - p_hat) / n)
ci_lower = max(0, p_hat - 1.96 * se)
ci_upper = min(1, p_hat + 1.96 * se)
p_range = np.linspace(0, 1, 1000)
likelihood = binom.pmf(k, n, p_range)
plt.figure(figsize=(12, 6))
plt.plot(p_range, likelihood, label='尤度関数')
plt.axvline(p_hat, color='r', linestyle='--', label='最尤推定量')
plt.axvline(ci_lower, color='g', linestyle=':', label='95%信頼区間')
plt.axvline(ci_upper, color='g', linestyle=':')
plt.xlabel('確率 p', fontsize=fontsize)
plt.ylabel('尤度', fontsize=fontsize)
plt.title(f'二項分布の最尤推定 (n={n}, k={k})', fontsize=fontsize)
plt.legend(fontsize=fontsize)
plt.grid(True, alpha=0.3)
plt.text(0.5, plt.ylim()[1], f'推定値: {p_hat:.3f}, 95%CI: ({ci_lower:.3f}, {ci_upper:.3f})',
horizontalalignment='left', verticalalignment='center_baseline', fontsize=fontsize)
plt.savefig('binomial_estimation.png', dpi=300, bbox_inches='tight')
plt.close()
# 例:100回中60回表が出た場合
plot_binomial_estimation(100, 60,fontsize=12)5. 限界
最尤推定法には以下のような限界や課題があります:
- モデルの誤特定:正しくないモデルを仮定すると、推定結果にバイアスが生じる
- 小標本での性能:サンプルサイズが小さい場合、漸近理論が適用できない
- 計算の複雑さ:複雑なモデルでは、尤度関数の最大化が計算上困難になることがある
参考文献
最終更新: