目次 / Contents
1. はじめに
私たちは日々様々な意思決定を行っています。
新しい治療法は本当に効果があるのか?広告キャンペーンは売上を増加させたのか?といった問に答えるためにデータを収集し、分析します。
しかしデータには常にばらつきがあり、完璧な答えを得ることは困難です。
ここで統計的推論、特に仮説検定と信頼区間が重要な役割を果たします。
コイン投げを考えてみましょう。
10回投げて7回表が出たとき、このコインは公平でしょうか?それとも偏りがあるのでしょうか?
この単純な例でも、確定的な答えを出すのは難しいことがわかります。
仮説検定と信頼区間は、このような不確実性に対処するためのツールです。
これらの手法を使うことで、データに基づいて信頼性の高い結論を導き出すことができます。
2. 仮説検定の基本概念
2.1 帰無仮説と対立仮説
仮説検定の出発点は、2つの競合する仮説を設定することです:
- 帰無仮説(H₀):通常、「差がない」「効果がない」といった保守的な立場を表します。
- 対立仮説(H₁):研究者が証明したい新しい主張を表します。
コイン投げの例では:
- H₀:コインは公平である(表が出る確率は0.5)
- H₁:コインは偏っている(表が出る確率は0.5ではない)
2.2 検定統計量とp値
仮説検定では、データから計算される検定統計量を用います。
この統計量は、帰無仮説が真である場合にどの程度起こりにくいかを数値化します。
p値は、帰無仮説が真であると仮定したとき、観測されたデータと同じかそれ以上に極端なデータが得られる確率です。
数学的には、p値は以下のように定義されます:
$$p=P(∣T∣≥∣t∣∣H0)p = P(|T| \geq |t| | H_0)p=P(∣T∣≥∣t∣∣H0)$$
ここで、$T$は検定統計量、$t$は観測された検定統計量の値です。
def plot_confidence_intervals(n_simulations, n_samples, true_mean, true_std):
"""Function to draw a simulation of a confidence interva"""
confidence_intervals = []
for _ in range(n_simulations):
sample = np.random.normal(true_mean, true_std, n_samples)
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1)
margin = stats.t.ppf(0.975, n_samples-1) * sample_std / np.sqrt(n_samples)
confidence_intervals.append((sample_mean - margin, sample_mean + margin))
fig, ax = plt.subplots(figsize=(12, 6))
for i, (lower, upper) in enumerate(confidence_intervals):
color = 'blue' if lower <= true_mean <= upper else 'red'
ax.plot([i, i], [lower, upper], color=color, alpha=0.5)
ax.axhline(true_mean, color='green', linestyle='--', label='true average')
ax.set_title('Simulation of 95% confidence intervals', fontsize=16)
ax.set_xlabel('Number of simulations', fontsize=12)
ax.set_ylabel('Estimates and confidence intervals', fontsize=12)
ax.legend(fontsize=10)
ax.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('confidence_intervals_simulation.png', dpi=300, bbox_inches='tight')
plt.close()
return Image('confidence_intervals_simulation.png')
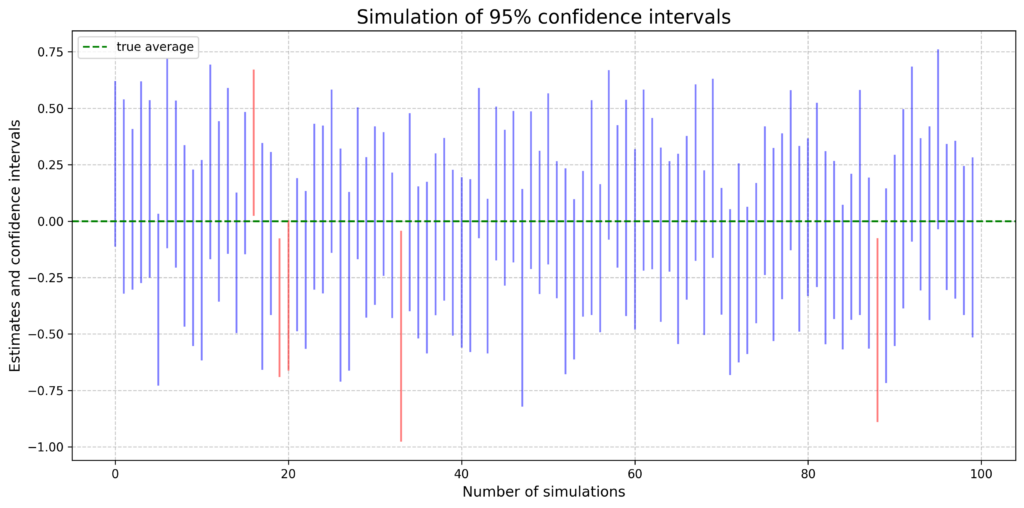
# 信頼区間のシミュレーション図の描画
plot_confidence_intervals(n_simulations=100, n_samples=30, true_mean=0, true_std=1)2.3 有意水準と検定の結論
研究者は事前に有意水準(通常α=0.05)を設定します。
p値がこの有意水準よりも小さい場合、帰無仮説を棄却し、対立仮説を採択します。
結論の解釈:
- p < α:「データは帰無仮説と矛盾する強い証拠を提供している」
- p ≥ α:「データは帰無仮説を棄却するのに十分な証拠を提供していない」
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import matplotlib.font_manager as fm
# 日本語フォントの設定
#fm.fontManager.addfont('/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc')
#fm._load_fontmanager(try_read_cache=False)
#plt.rcParams['font.family'] = 'Noto Sans CJK JP'
def plot_hypothesis_test(mean1, std1, mean2, std2, n, alpha=0.05, fontsize=12):
# データの生成
np.random.seed(42)
group1 = np.random.normal(mean1, std1, n)
group2 = np.random.normal(mean2, std2, n)
# t検定の実行
t_stat, p_value = stats.ttest_ind(group1, group2)
# プロットの作成
fig, ax = plt.subplots(figsize=(10, 6))
# ヒストグラムのプロット
ax.hist(group1, bins=20, alpha=0.5, label='Group 1')
ax.hist(group2, bins=20, alpha=0.5, label='Group 2')
# 平均値の垂直線
ax.axvline(np.mean(group1), color='blue', linestyle='dashed', linewidth=2)
ax.axvline(np.mean(group2), color='orange', linestyle='dashed', linewidth=2)
# ラベルとタイトル
ax.set_xlabel('Value', fontsize=fontsize)
ax.set_ylabel('Frequency', fontsize=fontsize)
ax.set_title('Hypothesis Test Visualization', fontsize=fontsize+2)
ax.legend(fontsize=fontsize)
# テキスト情報の追加
info_text = f't-statistic: {t_stat:.2f}\np-value: {p_value:.4f}\n'
info_text += f'Significant: {"Yes" if p_value < alpha else "No"}'
ax.text(0.95, 0.95, info_text, transform=ax.transAxes, fontsize=fontsize,
verticalalignment='top', horizontalalignment='right',
bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))
# 軸のフォントサイズ設定
ax.tick_params(axis='both', which='major', labelsize=fontsize)
plt.tight_layout()
plt.savefig('hypothesis_test.png', dpi=300, bbox_inches='tight')
plt.close()
from IPython.display import Image
return Image('hypothesis_test.png')
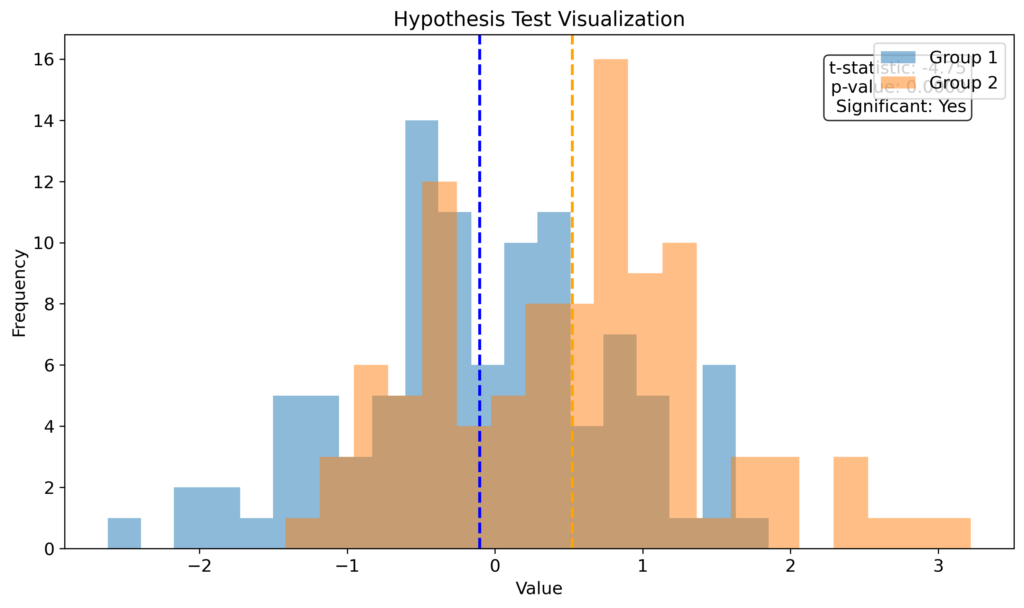
# 関数の実行
plot_hypothesis_test(mean1=0, std1=1, mean2=0.5, std2=1, n=100)3. 信頼区間の概念
信頼区間は、母集団パラメータの真の値が含まれる範囲を推定します。
通常、95%信頼区間が使用されることが多いと思います。
3.1 信頼区間の解釈
95%信頼区間の正確な解釈: 「同じ方法で多数の標本から信頼区間を計算した場合、その約95%が真の母数を含む」
この場合、特定の信頼区間が真の値を含むかどうかは常に確実ではありません。
3.2 信頼区間の計算(一般形)
多くの場合、信頼区間は以下の形式で表されます:
$$推定値±(臨界値)×(標準誤差)$$
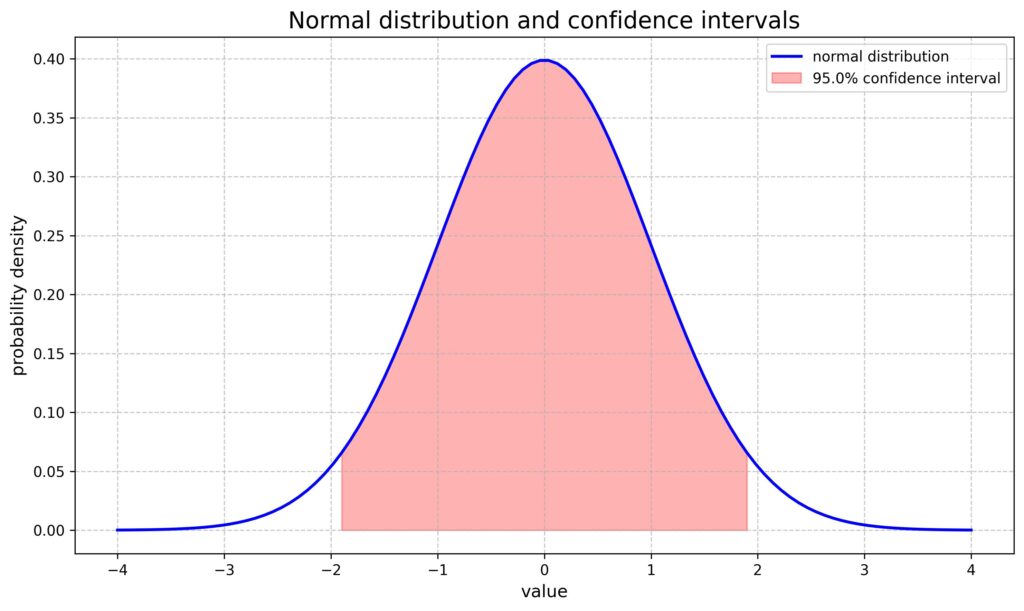
例えば、母平均μの95%信頼区間は:
$$\bar{x}±1.96 \times \frac{s}{\sqrt{n}}$$
ここで、$\bar{x}$は標本平均、$s$は標本標準偏差、$n$は標本サイズです。
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
import numpy as np
from scipy import stats
from IPython.display import Image
"""
# 日本語フォントの設定
fm.fontManager.addfont('/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc')
fm._load_fontmanager(try_read_cache=False)
plt.rcParams['font.family'] = 'Noto Sans CJK JP'
"""
def plot_normal_distribution(mean, std, alpha):
"""Functions for drawing normal distributions and confidence intervals"""
x = np.linspace(mean - 4*std, mean + 4*std, 100)
y = stats.norm.pdf(x, mean, std)
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, y, 'b-', lw=2, label='normal distribution')
ax.fill_between(x, y, where=(x >= mean - stats.norm.ppf(1-alpha/2)*std) &
(x <= mean + stats.norm.ppf(1-alpha/2)*std),
color='red', alpha=0.3, label=f'{(1-alpha)*100}% confidence interval')
ax.set_title('Normal distribution and confidence intervals', fontsize=16)
ax.set_xlabel('value', fontsize=12)
ax.set_ylabel('probability density', fontsize=12)
ax.legend(fontsize=10)
ax.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('normal_distribution.png', dpi=300, bbox_inches='tight')
plt.close()
return Image('normal_distribution.png')
# 正規分布と95%信頼区間の描画
plot_normal_distribution(mean=0, std=1, alpha=0.05)
4. 3つの主な仮説検定
仮説を検定するためのアプローチには、大きく以下の3つがあります。
4.1 尤度比検定
尤度比検定は、帰無仮説と対立仮説の下での尤度の比を考えます。
検定統計量:
$$\chi_{LR}^2 = 2[l(\hat{\theta}_1) – l(\hat{\theta}_0)]$$
ここで、$l(\hat{\theta}_1)$は対立仮説の下での最大対数尤度、$l(\hat{\theta}_0)$は帰無仮説の下での最大対数尤度です。
この統計量は漸近的に自由度$(p-q)$のカイ二乗分布に従います。
ここで、$p$は全パラメータ数、$q$は帰無仮説で制約されるパラメータ数です。
尤度比検定には以下の特徴があります。
- データと仮説の適合度を直接比較しているため、計算量が多い
- 小標本でも比較的信頼性が高い。
4.2 Wald検定
Wald検定は、最尤推定量の漸近正規性を利用します。
検定統計量:
$$\chi_{Wald}^2 = \hat{\beta}_0^T [Cov(\hat{\beta}_0)]^{-1} \hat{\beta}_0$$
ここで、$\hat{\beta}_0$は関心のあるパラメータの最尤推定量、$Cov(\hat{\beta}_0)$はその共分散行列です。
この統計量も漸近的に自由度$(p-q)$のカイ二乗分布に従います。
Wald検定には以下の特徴があります。
- 計算が比較的簡単。
- 大標本でよく機能するが、小標本では信頼性が低下する可能性がある。
4.3 スコア検定
スコア検定では、帰無仮説の下でのスコア関数(対数尤度の1次導関数)に注目します。
検定統計量:
$$\chi_{Score}^2 = U(\hat{\theta}_0)^T [I(\hat{\theta}_0)]^{-1} U(\hat{\theta}_0)$$
ここで、$U(\hat{\theta}_0)$は帰無仮説の下での最尤推定量におけるスコア関数、$I(\hat{\theta}_0)$はFisher情報行列です。
この統計量も同様に、漸近的に自由度$(p-q)$のカイ二乗分布に従います。
スコア検定には以下の特徴があります。
- 帰無仮説の下でのみ計算を行うため、計算量が少ない。
- 中程度の標本サイズでよく機能する傾向がある。
4.4 尤度比検定、 Wald検定、 スコア検定の比較
- 計算の複雑さ:
- 尤度比検定 > Wald検定 > スコア検定
- 必要な情報:
- 尤度比検定:帰無仮説と対立仮説の両方の下での最大尤度
- Wald検定:対立仮説の下での最尤推定量とその分散
- スコア検定:帰無仮説の下での情報のみ
- 標本サイズによる性能:
- 小標本:尤度比検定が比較的信頼性が高い
- 中程度の標本:スコア検定が効率的
- 大標本:3つの検定は漸近的に同等
- 不変性:
- 不変性とは、パラメータの変換(再パラメータ化)に対して統計量や検定の結果が変わらない性質を指します。
- 例えばθをパラメータとし、g(θ)を単調増加関数とします。
推定量T(X)がθの不変推定量であるとは、g(T(X))がg(θ)の推定量となることを意味します。 - 尤度比検定は、パラメータの再パラメータ化に対して不変です。
つまりパラメータをどのように表現しても(例:確率をオッズに変換するなど)、検定の結果は変わりません。 - Wald検定は一般に不変ではありません
- 計算の容易さ:
- スコア検定は帰無仮説の下でのみ計算するため、最も計算が容易
5. 具体例:臨床試験の分析
ECMOと従来療法の死亡割合を比較する臨床試験を考えます。
帰無仮説:$H_0: \pi_0 = \pi_1$(死亡割合に差がない) 対立仮説:$H_1: \pi_0 \neq \pi_1$(死亡割合に差がある)
ここで、$\pi_0$は従来療法の死亡割合、$\pi_1$はECMOの死亡割合です。
データ:
- 従来療法群:1人死亡、11人生存
- ECMO群:0人死亡、11人生存
尤度比検定を適用します。
各群の死亡数は二項分布に従うと仮定すると、尤度関数は以下のように表されます。
$$L\left(\pi_0, \pi_1\right)=\binom{12}{1} \pi_0^1\left(1-\pi_0\right)^{11} \cdot\binom{11}{0} \pi_1^0\left(1-\pi_1\right)^{11}$$
ここで、$\pi_0$は従来療法の死亡確率、$\pi_1$はECMOの死亡確率です。
計算を簡単にするために、対数尤度関数を使用します:
$$
\begin{aligned}
l\left(\pi_0, \pi_1\right) & =\log L\left(\pi_0, \pi_1\right) \\
& =\log \binom{12}{1}+\log \pi_0+11 \log \left(1-\pi_0\right)+\log \binom{11}{0}+11 \log \left(1-\pi_1\right)
\end{aligned}
$$
帰無仮説 $H_0: \pi_0 = \pi_1 = \pi$ の下では:
$$
l(\pi)=\log \binom{12}{1}+\log \pi+22 \log (1-\pi)
$$
最尤推定値は $\hat{\pi} = \frac{1}{23} \approx 0.0435$ となります。
$$
l(\hat{\pi})=\log \binom{12}{1}+\log \left(\frac{1}{23}\right)+22 \log \left(\frac{22}{23}\right) \approx-3.44
$$
対立仮説 $H_1: \pi_0 \neq \pi_1$ の下では:
$$
\hat{\pi}_0=\frac{1}{12} \approx 0.0833, \quad \hat{\pi}_1=0
$$
これらを代入すると:
$$
l\left(\hat{\pi}_0, \hat{\pi}_1\right)=\log \binom{12}{1}+\log \left(\frac{1}{12}\right)+11 \log \left(\frac{11}{12}\right)+\log \binom{11}{0}+11 \log (1)=0
$$
尤度比統計量を計算します。
$$
\chi_{L R}^2=2\left[l\left(\hat{\pi}_0, \hat{\pi}_1\right)-l(\hat{\pi})\right]=2[0-(-3.44)]=6.88
$$
自由度1のカイ二乗分布を用いて p値を計算します:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import matplotlib.font_manager as fm
# 日本語フォントの設定
fm.fontManager.addfont('/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc')
fm._load_fontmanager(try_read_cache=False)
plt.rcParams['font.family'] = 'Noto Sans CJK JP'
def plot_likelihood_ratio_test(chi2_stat, df=1, fontsize=12):
# カイ二乗分布の範囲を設定
x = np.linspace(0, 20, 1000)
y = stats.chi2.pdf(x, df)
# プロットの作成
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, y, 'b-', lw=2, label='カイ二乗分布 (df=1)')
ax.fill_between(x[x >= chi2_stat], y[x >= chi2_stat], color='r', alpha=0.5, label='p値')
# 統計量の位置を示す垂直線
ax.axvline(chi2_stat, color='r', linestyle='--', label='尤度比統計量')
# ラベルとタイトル
ax.set_xlabel('x', fontsize=fontsize)
ax.set_ylabel('確率密度', fontsize=fontsize)
ax.set_title('尤度比検定の視覚化', fontsize=fontsize+2)
ax.legend(fontsize=fontsize)
# p値とカイ二乗統計量の表示
p_value = 1 - stats.chi2.cdf(chi2_stat, df)
info_text = f'カイ二乗統計量: {chi2_stat:.2f}\np値: {p_value:.4f}'
ax.text(0.95, 0.95, info_text, transform=ax.transAxes, fontsize=fontsize,
verticalalignment='top', horizontalalignment='right',
bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))
# 軸のフォントサイズ設定
ax.tick_params(axis='both', which='major', labelsize=fontsize)
plt.tight_layout()
plt.savefig('likelihood_ratio_test.png', dpi=300, bbox_inches='tight')
plt.close()
from IPython.display import Image
return Image('likelihood_ratio_test.png')
# 関数の実行
plot_likelihood_ratio_test(6.88)$$
p=P\left(\chi_1^2 \geq 6.88\right) \approx 0.0087
$$
まとめると以下のようになります。
- 帰無仮説の下での対数尤度:$l(\hat{\pi}_0) = -3.44$
- 対立仮説の下での対数尤度:$l(\hat{\pi}_0, \hat{\pi}_1) = 0$
- 尤度比統計量:$\chi_{LR}^2 = 2(0 – (-3.44)) = 6.88$
- p値:$p \approx 0.0087 < 0.01$
ゆえに、有意水準5%で帰無仮説を棄却し、ECMOと従来療法の死亡割合に有意な差があると結論づけます。
しかし、この例では注意が必要です:
- サンプルサイズが小さいため、漸近近似の精度が悪い可能性があります。
- この試験では特殊な研究デザイン(アウトカム適応的ランダム化)が採用されており、単純な尤度比検定は適切でない可能性があります。
6. 応用
仮説検定と信頼区間は、医学研究、心理学、経済学、マーケティングなど、幅広い分野で活用されています。
例えば:
- 新薬の効果検証
- A/Bテストによるウェブサイトデザインの最適化
- 経済政策の効果分析
- 教育方法の比較評価
これらの手法を適用する際は、以下の点に注意が必要です:
- 適切な検定方法の選択(データの種類、分布の仮定など)
- 多重比較問題への対処
- 効果量の考慮(統計的有意性だけでなく、実質的な意義も重要)
- サンプルサイズと検出力の検討
7. 限界
仮説検定と信頼区間には、いくつかの限界や課題があります:
- 二分法的思考:p値による判断は、「有意」か「非有意」かの二分法になりがちです。
- サンプルサイズの影響:大きなサンプルサイズでは、実質的に意味のない差も統計的に有意になる可能性があります。
- 多重性の問題:多数の検定を行うと、偽陽性の確率が増加します。
- 発表バイアス:有意な結果のみが発表される傾向があります。
- 解釈の難しさ:p値や信頼区間の正確な意味は、専門家でも誤解しやすいものです。
参考文献
最終更新: