目次 / Contents
1. 導入
統計学の世界において最尤法(さいゆうほう、Maximum Likelihood Estimation, MLE)は、データから母集団のパラメータを推定するための最も重要な手法の一つです。
20世紀初頭にR.A. Fisherによって提唱されたこの方法は現代統計学の礎石となっています。
最尤法の基本的な考え方は「観測されたデータが最も起こりやすくなるようなパラメータの値を選ぶ」というもので、直感的にも理解しやすいものです。
2. 最尤推定の基本概念
2.1 尤度
尤度(ゆうど)は、観測されたデータが特定のモデルやパラメータのもとで生じる確率を表します。
直感的には、「このデータが得られる可能性はどのくらいか」を数値化したものと考えられます。
例えば、コインを10回投げて7回表が出たとします。
このとき、コインが公平(表が出る確率が0.5)である尤度と、不公平(表が出る確率が0.7)である尤度を比較することで、どちらの仮説がより妥当かを判断できます。
2.2 最尤推定の原理
最尤推定は、観測されたデータの尤度を最大にするパラメータを選ぶ方法です。
つまり「このデータが最も起こりやすくなるようなパラメータは何か」を推定します。
数学的には、パラメータ $\theta$ に対する尤度関数 $L(\theta)$ を最大化する $\theta$ を求めることになります:
$$\hat{\theta} = \arg\max_{\theta} L(\theta)$$
ここで、$\hat{\theta}$ は最尤推定量を表します。
2.3 対数尤度
実際の計算では、尤度関数の対数をとった対数尤度関数を使うことが多いです:
$$l(\theta) = \log L(\theta)$$
これには以下の利点があります:
- 数値的な安定性:尤度は非常に小さな値になることがあるため、対数をとることで計算が安定します。
- 計算の簡略化:積の対数は和になり、計算が簡単になります。
- 最適化の容易さ:対数関数は単調増加なので最大値の位置は変わりません。
3. 最尤推定の理論的基礎
3.1 スコア関数と情報量
最尤推定量を求める際、対数尤度関数の導関数(スコア関数)を用います。
スコア関数 $S(\theta)$ は、対数尤度関数 $l(\theta)$ のパラメータ $\theta$ に関する偏導関数です。
$$S(\theta) = \frac{\partial l(\theta)}{\partial \theta}$$
また、フィッシャー情報量は対数尤度関数の2階導関数の負の期待値として定義されます:
$$I(\theta) = -E\left[\frac{\partial^2 l(\theta)}{\partial \theta^2}\right]$$
3.2 スコア関数
$S(\hat{\theta}) = 0$ となる $\hat{\theta}$ が最尤推定量となる特徴があるため、最尤推定量を求める際に基本的なツールとなります。
とくに推定量の漸近的な性質を調べる際に重要です。
期待値がゼロ:$E[S(\theta)] = 0$、分散がフィッシャー情報量に等しい:$Var[S(\theta)] = I(\theta)$という特徴があります。
推定量の効率性や精度を評価し、適切な信頼区間を構築することができます。
3.3 フィッシャー情報量
推定量の精度を評価するための指標で、漸近分散の逆数となり、推定の効率を示します。
また、クラメール・ラオの不等式における下限を与えます。
非負定値($I(\theta) \geq 0$)、加法性(独立なサンプルの情報量は加算的)、スコア関数の分散に等しい($I(\theta) = Var[S(\theta)]$)という特徴があります。
スコア関数と情報量の関係:
- 推定効率:情報量が大きいほど推定の精度が高くなります。
- 漸近正規性:最尤推定量の分布は $N(\theta, I(\theta)^{-1})$ に漸近します。
- Wald信頼区間:$I(\theta)^{-1}$ は標準誤差の推定に用いられます。
最尤推定の理論的基礎を形成し、推定量の性質を理解し評価する上で重要な役割を果たします。
3.4 最尤推定量の性質
最尤推定量には、以下のような望ましい性質があります:
- 一致性:サンプルサイズが大きくなるにつれ、真の値に確率収束します。
- 漸近正規性:大標本においては正規分布に従います。
- 漸近有効性:大標本においては不偏推定量の中で最小の分散を持ちます。
これらの性質により、最尤推定量は多くの状況で優れた推定量として機能します。
4. 信頼区間の基本概念
4.1 信頼区間
信頼区間は推定量の不確実性を定量化するツールです。
例えば95%信頼区間は「真のパラメータ値がこの区間に含まれる確率が95%である」ことを示します。
形式的には、パラメータ $\theta$ の $(1-\alpha)100%$ 信頼区間 $[L, U]$ は以下を満たします:
$$P(L \leq \theta \leq U) = 1 – \alpha$$
ここで、$\alpha$ は有意水準(多くは5%や1%)です。
4.2 Wald信頼区間
最尤推定と組み合わせてよく使われるのがWald信頼区間です。
これは信頼区間の一種で、最尤推定量の漸近正規性を利用しています。
統計解析で一般的に用いられる信頼区間はWald型のものを指す場合が多く、多くの統計モデル(線形回帰、ロジスティック回帰など)でパラメータの推定にWald信頼区間が使用されます。
$\theta$ の Wald 信頼区間は以下のように構築されます:
$$[\hat{\theta} – z_{\alpha/2} \cdot SE(\hat{\theta}), \hat{\theta} + z_{\alpha/2} \cdot SE(\hat{\theta})]$$
ここで、$z_{\alpha/2}$ は標準正規分布の上側 $\alpha/2$ 点、$SE(\hat{\theta})$ は $\hat{\theta}$ の標準誤差です。
4.3 信頼区間とWald信頼区間の違い
| 信頼区間 | Wald信頼区間 |
| より一般的な概念で、様々な方法で構築できる統計的区間を指す。 | 信頼区間の一種で、特定の仮定と方法に基づいて構築される。 |
| 様々な分布や状況に適用可能。 | 主に大標本で、推定量が正規分布に従う(または近似できる)場合に適用される。 |
| 様々な手法(ブートストラップ法、尤度比法など)で構築可能。 | 最尤推定量の漸近正規性を利用し、 推定量±(臨界値×標準誤差)の形で構築。 |
| 状況に応じて適切な方法を選択でき、より正確な結果が得られる場合がある。 | 大標本では良好だが、小標本や特定の状況では精度が低下する可能性がある。 |
簡潔に言えば、Wald信頼区間は信頼区間の一種で、特定の仮定と方法に基づいた比較的簡単な構築方法を持つ区間です。
一般的な信頼区間はより広い概念で、様々な状況に適応できる柔軟性を持っています。
Wald信頼区間は計算が非常に簡単で、最尤推定量と標準誤差さえ分かればすぐに計算できます。
これは特に複雑なモデルや大規模なデータセットを扱う際に有用です。
またWald信頼区間は推定値を中心とした対称な区間として表されるため、解釈が直感的にできます。
これらがWald信頼区間が多用される主な理由です。
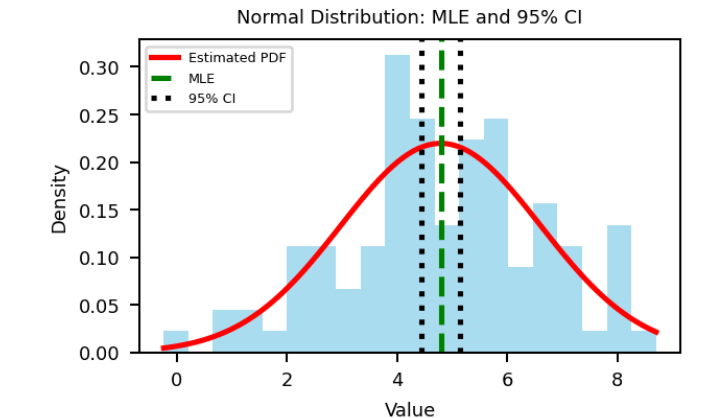
5. 具体的な例:正規分布の平均の推定
正規分布 $N(\mu, \sigma^2)$ からのサンプル $x_1, \ldots, x_n$ が得られたとき、$\mu$ の最尤推定量と信頼区間を求めてみます。
5.1 最尤推定量の導出
対数尤度関数は以下のようになります
$$l(\mu, \sigma^2) = -\frac{n}{2}\log(2\pi\sigma^2) – \frac{1}{2\sigma^2}\sum_{i=1}^n (x_i – \mu)^2$$
$\mu$ について偏微分してゼロとおくと
$$\frac{\partial l}{\partial \mu} = \frac{1}{\sigma^2}\sum_{i=1}^n (x_i – \mu) = 0$$
これを解くと、$\mu$ の最尤推定量が得られます
$$\hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i$$
つまりサンプル平均が最尤推定量となります。
5.2 信頼区間の構築
$\hat{\mu}$ の標準誤差は $SE(\hat{\mu}) = \sigma/\sqrt{n}$ です。
これを用いて、95%信頼区間は以下のように構築されます:
$$[\hat{\mu} – 1.96 \cdot \frac{\sigma}{\sqrt{n}}, \hat{\mu} + 1.96 \cdot \frac{\sigma}{\sqrt{n}}]$$
ここで、1.96 は標準正規分布の97.5パーセント点です。
6. 応用
最尤推定と信頼区間は、様々な分野で広く応用されています:
- 医学研究:新薬の効果の推定と信頼区間の報告
- 経済学:経済指標の推定と予測区間の構築
- 機械学習:モデルパラメータの推定と不確実性の評価
- 品質管理:製品の不良率の推定と管理限界の設定
これらの手法は、ベイズ推定や最小二乗法など、他の統計手法と比較されることもあります。
それぞれに長所短所があり、問題の性質に応じて適切な手法を選択することが重要です。
7. 限界
最尤推定と信頼区間には、以下のような限界や課題があります:
- サンプルサイズの影響:小標本では性質が保証されない場合がある
- モデルの誤特定:誤ったモデルを仮定すると、推定結果が信頼できない
- 計算の複雑さ:複雑なモデルでは、最適化が困難になることがある
- 信頼区間の解釈:頻度論的解釈と直感的理解のギャップ
これらの課題に対処するため、ロバスト推定法やブートストラップ法など、様々な拡張や代替手法が研究されています。
8. 結論
最尤推定と信頼区間は、不確実性を含むデータから情報を抽出し、その精度を評価するための強力なツールです。
これらの手法を理解し適切に使用することで、より信頼性の高い統計的推論が可能になります。
- 尤度は、データがモデルに適合する度合いを表す
- 最尤推定は、データを最もよく説明するパラメータを選ぶ
- 信頼区間は、推定の不確実性を定量化する
- これらの手法は様々な分野で広く応用されている
- 限界を理解し、適切に使用することが重要
参考文献
最終更新: